
بعد ان عرفنا بعض المفاهيم الاساسية جدا وبصيغة بدائية جدا ، منها ( مفهوم نظرية التعقيد Complexity Theory ) و (مفهوم تحسين الحلول Optimization) ، سنكمل الان محطة اخرى من هذه الرحلة لنتوسع بالمفهوم اكثر ، ونتعرف اكثر الى هذا العالم المجهول بالنسبة للكثيرين . هذا العالم موجود لدينا ونعيشه دائما ولكننا لم ننتبه لوجوده، والسبب اننا لا نعرف بانه حقيقة علمية موجودة ، عشناها في مراحلة من حياتنا الشخصية . على سبيل المثال ، الاغلب منا كان والده يوصله الى المدرسة بسيارة العائلة ، وكان الاخ او الاخت ايضا من ضمن الافراد الموجودين ضمن قائمة الركاب ، لكن طريق المدرسة لا يلتقي مع طريقة الجامعة (مثلا ) ، والاثنين بعدين عن طريق عمل الوالد ، هنا كيف سيقوم الوالد باخذ افضل الطرق التي من الممكن ان تربط الثلاثة معا باقل تكلفة وقت ووقود ؟! . في واقع الحال ، نقول ان اي طريق يتخذه من الممكن ان يؤدي الغرض للجميع ، سواء اذا اوصل الصغير الى المدرسة ثم الفتاة الى جامعتها ، ثم يمضى بعدها في طريقه الى عمله ، او العكس ايضا ، ولكن بعد ان عرفنا ان هنالك مايسمى بنظرية التعقيد ، والتي عقدت لنا الامور كثيرا ، اصبح من واجب الاب الواعي ان يبحث في اي الطرق التي ستؤدي له عن افضل وقت لكي يصل عمله وايضا لكي يلتحق ابناءه بدراستهم ، وكذلك اقل تكلفة في الوقود .
هذه المشكلة واقعية جدا ، ولطالما حدثت وتحدث ، وقد تم تصنيفها ضمن مشكلتين اساسيتين ، الاولى منها ضهرت مع عالم الرياضيات ومكتشف نظرية مخططات Graph Theory المعروف (اويلر Euler ) سنة 1737 . عندما كان في زيارة لمدينة ( اويزنبرك KÄonigsberg ) . كانت المدينة تقع على ضفتي نهر . وتربط بينها سبعة جسور ، ونهاية كل جسر عبارة عن منطقة جديدة ، الشكل التالي يوضح خريطة المدينة ببساطة : –

نلاحظ من الشكل ان هنالك اربع مناطق ، كل منطقة يخرج منها جسر ويعود اليها جسر اخر ، اذن لكل منطقة جسرين مرتبطين معها ، ماعدا المنطقة B والتي هي مرتبطه مع الثلاث مناطق الاخرى بثلاثة جسور . المشكلة التي حصلت معه ، انه كان يريد ان يزور كل منطقة من المناطق الواقعه عند نهاية الجسور ، على ان يمر على كل جسر مرة واحدة – اي من دون ان يستخدم نفس الجسر مرتين – وفي النهاية يعود الى المنطقة الاولى التي انطلق منها . وجد اويلر انه امام معضلة لم يستطع حلها ، وهو انه من اي منطقة سيبدأ ؟ وماهي المنطقة التالية ؟ وماهي التي تليها ؟ وهل انه يستطيع ان يعبر كل جسر مرة واحدة ؟ وهل سيعود الى المنطقة التي بدأ منها ؟ . اسئلة كثيرة ظهرت له ، كانت صعبة جدا عليه . استدعت منه ان يبتكر لنا جزءا مهما ومفهوما اصبح رئيسيا في كثير من العلوم الرياضية وفي الرياضيات المتقطعة Discreet Mathematics ومفهوم حل المشاكل المستعصية ( الذي نحن نتحدث عنه ) . اسماها Graph Theory والسبب هو لان مثل نهاية كل جسر بدائرة ، والجسور التي تربط بين هذه المناطق هي عبارة عن خطوط توصيل او نقل . نطلق على الدوائر Vertex اما الخطوط فنطلق عليها Edge . اسميت هذه المشكلة بمشكلة اويلر او Eulerian trail او Eulerian tour ، وهذه اسميت في بعض الاحيان باسم المدينة الاصلية KÄonigsberg problem .
لذلك يكون لدينا ثلاثة تعاريف للمشكلة حسب الشكل Graph :
1- مسار اويلر Eulerian trail : اذا تم الانطلاق من نقطة والانتهاء بنقطة اخرى مختلفة مع زيارة جميع الخطوط التي تربط بين المناطق التي تمت زيارتها مرة واحدة، عند ذلك نقول ان الشكل Graph يحتوي على مسار اويلر .
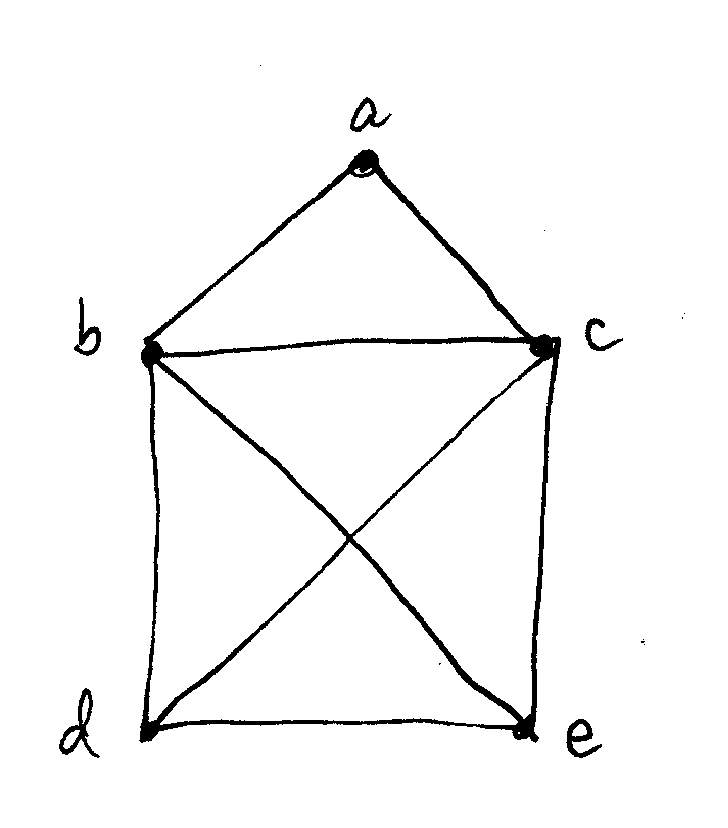
2- حلقة اويلر Eulerian Circuit : اذا تم الانطلاق من نقطة معينة ، والانتهاء بنفس النقطة مع زيارة جميع الخطوط التي تربط بين المناطق التي تم زايرتها مرة واحدة ، عند ذلك نقول ان الشكل Graph يحتوي على حلقة اويلر .
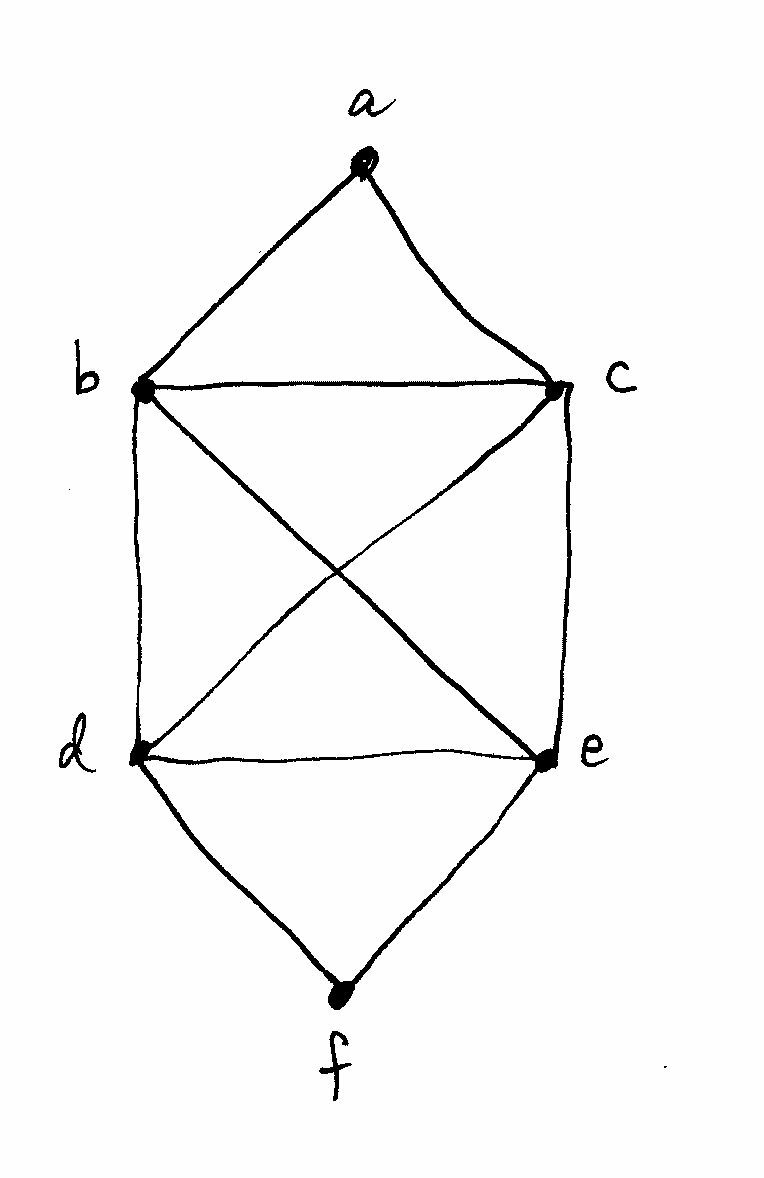
بعد ان قام بتوصيف الحل بسكل Graph ، وجد ان اول طريقة من الممكن ان تساعده بالحل هي عدد المخارج والمداخل لكل منطقة ، فوجد ان الشكل الذي تكون مناطقه مرتبطة بعدد زوجي من الخطوط ، فانه يحتوي على حلقة اويلر ومن الممكن ان يقوم بزيارة كل المناطق من خلال كل الجسور مرة واحدة ويعود الى نفس المنطقة الاصلية . هذه المشكلة وضعت لها اليات وفرضيات كثيرة لغرض اقتراح طرق لحلها ، واساس حلها كما ابتكرها اويلر نفسها هو الاعتماد على درجة الشكل – اي عدد الخطوط الصادرة – هل هو زوجي ام فردي . لكن هنا لم نلاحظ انه تأثر بالوقت ، او قال ان زيارة المنطقة C يجب ان تكون ضمن افضلية اكثر من المنطقة الاخرى ، ولذلك هذه المشكلة نطلق عليها ( مشكلة غير موزونة Unweighted Graph . والسبب انني لا اعرف كم هو طول الجسر الذي يربط بين A و D ، ولا اعرف كم من الوقت ساستغرق لزيارة B من C . المطلوب هو زيارة جميع المناطق من خلال زيارة كل جسر مرة واحدة فقط .
الحديث اعلاه كان حول المشكلة الاولى وهي مشكلة اويلر ، اما الان فلدينا المشكلة الثانية والتي هي من المشاكل المعقدة جدا والتي تعاني لحد الان من عدم وجود حل شاف لها . الا وهي مشكلة حلقة هاملتون Hamiltonian Cycle . اول ظهور هذه المشكلة كان عبارة عن لعبة قام بابتكارها السير وليام هاملتون سنة 1856 اسماها Icosian من الممكن ان نلفظها ايقوسيا ، وارسلها لصديقه لكي يلعبها في وقت فراغه ويجد نفسه هل يستطيع حلها ، لم يعلم في وقته انه وضع لعبة لم تحل حتى اليوم .

كما موضح في الشكل السابق ، لعبة او مشكلة هاملتون كانت عبارة عن لوح يحتوي على 20 منطقة ، متصله مع بعضها بخطوط كما هي موضحه ، قاعدة اللعبة الوحيدة تقول : اذا اخترت نقطة للبداية ، هل تستطيع ان تزورج جميع المناطق من خلال جميع الخطوط الموجودة مرة واحدة دون تكرار نفس المنطقة مرتين ؟ والعودة الى النقطة الاولى التي بدأت منها ؟
الصورة التالية توضح احد الحلول الممكنة للغز :

بعد ان حاولت ان تكتشف الخطوط الواصلة بين النقاط ، وحاولت ان تبحث عن الحلقة ، كم هو عدد الحلقات التي تستطيع ان ترسمها وفقا للشرط المذكور اعلاه ؟ مع الاخذ في كل مرة نقطة بداية مختلفة .
على سبيل المثال :

في الشكل اعلاه ، من الممكن ان تبدأ الرسم من النقطة 1 ، وتتجه في كل الاتجاهات بحثا عن الحلقة المطلوبة ، سنجد ان هنالك حلقتين ، الاولى هي المسار (1 5 4 3 2 8 7 6 ) والثانية عكس المسار المذكور . ولنلاحظ ان المسار الذي ينطلق من 1 ثم الى 2 لا يمكن ان يكون حلقة ، ولذلك لا يتم ذكره في النتائج .
مئات البحوث طرحت منذ 150 سنة وحتى الان ، تحاول في حل هذه المشكلة من خلال وقت معلوم . ولكن حتى الان المسألة تعتبر معضلة للجميع . وكما قلت سابقا مع مشكلة اويلر ، بما اننا لم نكترث الى المسافة الفاصلة بين نقطة واخرى ، وكذلك الى الزمن الذي نستغرق عند الذهاب من نقطة الى اخرى داخل شكل هاملتون ، فان هذا المخطط Graph ايضا يعتبر غير موزون Unweighted .
الاختلافات بين هاملتون وايولر قليلة وقد تعطي للبعض انطباع بانهما متشابهين ، الا ان هنالك فرق جوهري بينهما وهو ، في مشكلة اويلر تتم الزيارة من خلال جميع الخطوط الواصلة بين النقاط مرة واحدة فقط ، من الممكن تكرار المناطق . اما في مشكلة هاملتون لايمكن زيارة منطقة معينة لاكثر من مرة ، الشرط هو يجب زيارة جميع المناطق مرة واحدة ، اما بالنسبة للخطوط الفاصلة فانه ليس من الضروري استخدامها كلها ، وانما فقط الذي يخدمنا منها .
من خلال مشكلتي اويلر وهاملتون ، نجد بان الوالد لو اراد ان يوصل ابناءه الى اماكن دراستهم جميعا ، اصبح من الواجب اولا ان يبحث في امكانية وجود طريق يرجعه الى مكان عمله . وهذه نقطة اساسية ، قبل التفكير في التكلفة الاقل والزمن الاقل . لذلك ، وبعد ان عرفنا ان هنالك مشاكل قديمة جدا اعتبرتها نظرية التعقيد الحسابي كنماذج لمشاكل يومية نمر بها ، اصبح من الواجب التفكير في اي الطرق نسلك .؟ وايهما افضل ؟ وان كانت مشكلة هاملتون معضلة عمرها 150 سنة ، الا ان الوالد سيوصل الجميع الى اماكن دراستهم بسلام ، ويطمئن عليهم ويذهب هو الى عمله بسلام ايضا . ونستنتج ايضا بان كل الطرق قد ادت الى روما ، ولكن ليست بعشوائيه وانما من خلال بحث علمي مدروس .
الى هنا سنتوقف في رحلتنا قليلا ، الى محطة اخرى قادمة نوضح من خلالها كيف يكون الشكل الموزون وتأثيره على المشاكل . اتمنى ان تكون هنالك فائدة علمية للجميع بعد قراءة هذه المقالة المبسطة .
تحياتي العطرة ..
سنان محمد صالح ..
