Fawzy Hageb 

 أتذكر جيدا تلك الايام التى كنت حينها فى عمر الـ 5 و الـ 6 حينما كنت أكثر زملائي تفوقا فى قدرة عد الاعداد . كنت أستطيع العد الى أكثر من 10000 !!  ولكن الى أى مدى أستطيع الاستمرار ؟؟ وما هى أكبر الاعداد ؟؟

تطلبت الاجابة على هذة الاسئلة رحلة رياضاتية عظيمة على مر التاريخ  . حيث تبلورت فيها أفكار تناقضت مع المنطق بشكل صريح رغم انها نتاج المنطق ذاتة !! انها رحلة اللاعودة . انها رحلة اللانهاية ….  

لنبدأ مع سؤال . الى اى مدى نستطيع العد ؟ ومتى سنتوقف ؟

لنفرض ان شخصا قد بدأ العد من لحظة الانفجار العظيم متى يستطيع ان ينتهى من عد كل الارقام ؟ أم انة لن يتوقف مطلقا ؟؟

يبدو وللوهلة الاولي ان الامر لن ينتهى فانت تستطيع ان قلت ان 100000000 هو اخر عدد ولا استطيع ان اعد اكثر من ذلك انت تستطيع ان تضيف 1 الى هذا الرقم وبتكرار هذه  العملية ستجد انك تستطيع ان تعد حتى تموت او حتى الى نهاية الكون – هذا ان كان له نهاية و لا تقلق فلن تحيا مدة كافية لتشهد هذه الحادثة الرهيبة ان حصلت فى كل الاحوال –

من هنا نجد ان الاعداد تمتد الى اللانهاية اي  بمعنى اخر لا يوجد لها حد نهائي عندما تصل له تقل لك “قف”

ولكن لو اخذنا مثلا مجموعتين مختلفتين من الارقام و كمثال

مجموعة الاعداد الزوجية –هىتلك الاعداد التى تقبل القسمة على 2 او بمعنى اخر هى الاعداد التى تكون احدا عواملها الاولية 2 — 

ومجموعة الاعداد الطبيعية – 1و2و3و4و…….. –

فاي مجموعة هى الكبرى ؟؟

من المعلوم جيدا اننا نستطيع ان نكمل العد الى الابد من خلال كلا المجموعتين ولكن هل هما متساويتان ؟؟ ام هناك مجموعة اكبر من الاخرى ؟؟؟

يبدو سؤالا مستحيل الاجابة علية و لكننا سنجيبه على اية حال .. لكن قبل ذلك دعونا ناخذ جولة فى التاريخ !

لنفرض ان شخصا لا يعرف من الاعداد الا 8 اعداد فقط وهم 1 و 2 و 3 و 4 و 5 و 6 و 7 و 8 و9

وهذا الشخص قد دخلت قبيلته في معركة ما ( اذ انى لا اتوقع ان شخصا ما لا يعرف الا 9 اعداد يعيش فى عالم متمدن كهذا ) وعلى اية حال لا تقلق ولا تستغرب من هذا المثال فقبائل الهونتوت لا تعرف الا 3 اعداد فقط وهم 1 و 2 و 3 – حيث ان مستكشفي اوروبا الذين استكشفوا هذة القبائل لم يجدوا فى مفردات لغتهم الا 3 اعداد فقط !! –

فكيف يستطيع ان يحصر عدد القتلى و عدد الناجين ؟؟ اذا تم توجيه السؤال الاتي له ” أيهما أكبر عدد الموتى ام الناجين ؟؟ ” فما سيفعل ؟؟

اتوقع ان كان على درجة عالية من الذكاء فانة سيرمز لكل قتيل بقطعة من الحصي و لكل ناجى بنوع اخر من الحصي و يضع كلا منهما على جانبين و يحذف كل حصاة مع واحدة من النوع الاخر فاذا تبقي بعض من احد النوعين كان هذا الفريق الذي يرمز له اكبر و اذا انتهيا مع بعضهما فيكون الفريقان متساويان ..

ولما كانت لغتنا لا تستطيع ان تتعامل مع اللانهايات– ولا حتى عقولنا – فدعنا نفعل ذلك ..

أيهما أكبر ؟ مجموعة الاعداد الطبيعية ام الزوجية ؟؟

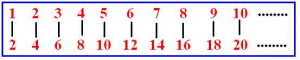
هنا سنعتمد أسلوب أهل الهونتوت بأن نقابل كل عدد زوجي مع عدد طبيعي ونري أيهما سيكون أكبر و أيهما سينتهى أولا ..

وكما نري فى الشكل اننا امام كل عدد زوجي سيوجد عدد صحيح و العكس ايضا صحيح واذا استمرينا الى الابد فسيكون نفس الحال اى انه سنجد انه مع كل عدد صحيح سنزيل كل عدد موجب اي اى المجوعتان متساويتان ..

ولكن مهلا عزيزي القارئ ..

هل حقا هما متساويتان ؟؟ دعنا نفكر قليلا و اتمنى ان تسترجع معى بديهيات اقليدس

ألا تتذكر واحدة تقول ” أن الكل اكبر من الجزء ؟ ” وكمثال انت انسان لنفرض انك كل تملك راس هذا الراس جزء من جسدك ككل صحيح ؟

حسب البديهية فانت كانسان اكبر من الراس لانه جزء اكبر منه حجما و ثقلا و كل شئ ..

دعنا نطبق ذلك على الارقام ..

حسبما تري فان كل عدد بالصف الثانى– الاعداد الزوجية – تجدها ايضا فى الصف الاول – الاعداد الطبيعية – اذا فهي حتما جزءا منها و من المعروف ان الاعداد الزوجية هى مجموعة جزئية من الاعداد الطبيعية فكيف تكونان متساويان ؟؟ أليس هذا تناقضا عجيب مع البديهة و المنطق ؟؟ ولكن هذا ما أوصلنا الية المنطق !!

وأحمد الله ان هذه البديهة تنطبق على الكون عموما لانها لو كانت لا تنطبق على هذا الكون لما كنت انا او انت هنا ولكن دعنا من هذا فاعدك فيما بعد ان اتحدث عن هذا الموضوع بالتفصيل ..

الان وجدنا ان مجموعة الاعداد الزوجية = مجموعة الاعداد الطبيعية ..

لكن . هل كل المالانهايات متساوية ؟؟

فى الحقيقة الاجابة هى كلا .. هناك مالانهايات اكبر من مالانهايات اخري !! واعرف ان هذا يبدو مصادما للمنطق !

ولكن ما هى تلك الانهايات الاكبر من الانهايات الاخري ؟

أحد تلك اللانهايات هى لانهائية الاعداد الحقيقية ولا نهائية الاعداد العشرية الغير دورية و الغير منتهية !

سنتناول فيما يلي برهان يثبت لنا ان مالانهاية عدد النقاط على خط هندسي اكبر من لانهاية الاعداد الطبيعية ..

وبنفس منطق رجل الهونتوت سنقوم بالمقارنة بين العناصر كما فعلنا من قبل و لكن قبل ذلك سنقارن ماذا مع ماذا ؟!

لو فرضنا اننا عندنا خط هندسي كالاتى طولة = 2 متر

فاني اتسائل .. ما هى بعد النقطة س عن احد طرفي القطعة المستقيمة ؟؟

يحتمل ان تكون 0.5 وان تكون 0.1 وان تكون 0.9999 وان تكون جذر 2 متر من احد الطرفين

وكما قلت يحتمل ان تكون جذر2 متر من احد الطرفين صحيح ؟؟

كما يعرف الجميع ان جذر 2 احد الجذور الصماء – وسوف تناول هذا الامر فى احد المواضيع فيما بعد –

وهو عدد عند تمثيلة نجد انه على يمين العلامة العشرية لا توجد نهاية للارقام على يمين العلامة العشرية وايضا لا توجد دورية على يمين العلامة العشرية – بمعنى ان الارقام لا تتكر على اليمين كل عدد معين من الارقام كمثل 2/3 مثلا –

الان اذا نستخلص النتيجة الاتية ..

بعد النقطة س عن احد الطرفين يمكن ان ياخذ اي قيمة عددية حقيقية كمثل الجذور مثلا …

الان نبحث هل لانهائية الجذور الصماء – او الاعداد العشرية الغير منتهية و الدورية – أكبر ام اصغر من لانهائية الاعداد الطبيعية ؟؟

فاذا اثبتنا ان لانهائية الاعداد العشرية الغير منتهية اكبر من لانهائية الاعداد الطبيعية نجد بالتالى ان لانهائية قطعة مستقيمة اكبر من لانهائية الاعداد الطبيعية والعكس صحيح ..

كما ذكرت انفا سنعود الى طريقة رجل الهونتوت

وهذة الاستدلال الذي سنستخدمة بـ ( حجة كانتور القطرية )

لنفرض أن شخصا أدعى انة يمكن ان نقارن كل رقم طبيعي بكل رقم عشري غير منتهى و اعطانا كمثال الشكل التالى

 

فى هذة الحالة دعنا نقل له الاتى لنضع عدد جديد بحيث يكون مختلف مع الرقم الاول فى الخانة الاولي بعد العلامة ومع الثانى مع الخانة الثانية بعد العلامة و مع الثالث فى الخانة الثالث بعد العلامة فيكون

0.88304…………..

او

0.92060 ………..

او اية رقم طبقا للقاعدة المذكورة و لنفرض انة قال ان هذا الرقم ستجده مقابل رقم 510 فى هذه الحالة نذهب للخانة رقم 510 بعد العلامة من الرقم الجديد و نغيرة عن الرقم المقابل لـلخانة 510 من الرقم !!

لكم ما فائدة هذه الطريقة ؟؟

فائدة هذه الطريقة فى ايجاد الارقام الجديدة هى انها تعطينا ارقام لا توجد فى السلسلة المقابلة للارقام الطبيعية و بالتالى نجد انه مع كل رقم طبيعي هناك مالانهاية من المالانهايات من الارقام العشرية الغير منتيهة  !!

وبهذا نجد ان مجموعة الارقام العشرية الغير منتهية و الغير دورية أكبر من مالانهاية  الاعداد الطبيعية و بالتالى فان عدد النقاط على قطعة مستقيمة اكبر من الارقام الطبيعية كلها !!

فى المرة القادمة سنتحدث عن

–         مفارقة الفندق اللانهائي وحاصل جمع لانهائيتان

–         لانهائية الاعداد الكسرية و الاعداد الطبيعية

–         لانهائية نقاط القطع المستقيمة و المستويات و الفضاءات المتعددة الابعاد..

 المراجع

 النسخة المترجمه عن كتاب

1 2 3 4 5 …. Infinity

بعنوان ” بداية بلا نهاية ”

 وثائقي من انتاج بي بي سي بعنوان :Infinity