بداية يجب أن أسجل حقوق العنوان للسيد (سين ـ ليقي ـ اونني) جامع ( أو مؤلف ) ملحمة كلكامش حسب (طه باقر ـ ملحمة كلكامش) , حتى لا نسلب الناس أشيائهم .
رؤيا بوانكارييه
الذكرى الستين (1889م) لولادة اوسكار الثاني ملك السويد والنروج أراد لها الملك ومستشاريه أن تكون متميزة علمياً ،فأعلن البلاط الملكي تقديم جائزة مقدارها (2500 كرونة )لمن يستطيع ان يأتي بنموذج رياضي يثبت فيه استقرار النظام الشمسي , فحسب قوانين نيوتن السائدة تلك الأيام، كان على النظام الشمسي أن يسير برتابة واستقرار ما بقي الكون.
انبرى لهذه المهمة بروفسور الرياضيات بجامعة باريس هنري بوانكارييه (Henri Ppincare’ ) , لبوانكارييه الذي حاز على شهادة من برتراند راسل كأفضل من أنجبتهم فرنسا إسهامات كبيرة بالتبولوجيا (Topology) ـ علم دراسة الصفات الهندسية التي لا تتغير بالشد دون التمزيق أو الهندسة المرنة ـ ,التحليل الرياضي , الفيزياء النظرية وغيرها.
هنري بوانكارييه ابتدأ حله (النموذج الرياضي) بافتراض وجود ثلاث كواكب بمستوي يفترض إن اثنين منهما كبيران والثالث صغير جداً بالنسبة لهما،ولتكن تلك الكواكب الشمس , الأرض و القمر مع افتراضات بإهمال أمور لم يعتقد بوانكارييه بأهميتها بالحل سيراً على المقولة الشائعة “إذا كنت تحسب حركة كرة بلياردو فليس لك ان تأخذ بعين الاعتبار سقوط صخرة ما على كوكب في إحدى المجرات” , استطاع بوانكارييه ان يجد نموذجا لدوران الأجسام الثلاثة وهو يعتبر تعميم لدوران جسمين حول بعضهما التي كانت تعتبر محلولة وقتها , سميت هذه المسألة في ما بعد بمسألة الأجسام الثلاثة (three body problem) .
لكن قبل نشر الورقة البحثية التي تحتوي النموذج من قبل (ميتاغ ليفلر-المستشار العلمي للملك أوسكار) طلب منه بوانكارييه التوقف عن النشر، كان بوانكارييه قد اكتشف حساسية كبيرة لموقع الأجسام الإبتدائي على سلوكها الحركي واكتشف إن ما اهمله (ضناً منه بأنه غير مهم) بالحسابات كان ليقلب النتائج رأس على عقب رغم إن بوانكارييه لم يجد نموذجا نهائيا لدوران الأجسام الثلاثة إلا أن اسلوبه بمعالجة المسألة جعله يفوز بجائزة اوسكار الثاني ، لقد كان بوانكارييه يعتقد إن مزيد من الدقة بالحسابات قد تخلصه من الحساسية للمواقع الابتدائية , لم يكن أفضل من انجبته فرنسا يعلم بأن الحساسية تلك من صفات النظام نفسه وليست دخيلة عليه , رغم عقليته الهائلة وأفكاره الرياضية المثيرة كان بوانكارييه محكوم بأفكار نيوتن ولابلاس حول الحتمية كان مؤمن بمبدأ التقارب القائل “إذا ما أعطينا الفروق التقريبية المبدئية لنظام ما والقوانين التي تحكمه فيمكننا أن نتوصل إلى نتائج تقريبية لنظام ما ” لكن ما مدى صحة هذه العبارة ؟
لورنز وتأثير الفراشة
كان ادورد لورنز (Edward Lorenz) مع موعد لتغيير قدره العلمي عام 1938 عندما عين بمعهد ما سوشوستس للتكنلوجيا (Massachussets Institute of Technology) في مجال التنبؤ بالتطقس كان لورنز حسب (جيمس جلايك ـ الفوضى تصنع علماً جديد ) رياضي ملتحف بعباءة التنبؤ بالطقس .
بشتاء 1961 كان لورنز متعباً ً من حرارة حاسوبه فقرر أن يختصر الوقت ويدخل نتائج سابقة كمدخلات أولية لحساب بيانات الطقس وبعد فنجان قهوة بعيداً عن صوت الحاسبة وحرارتها المزعجة تفاجئ لورنز بالنتائج حيث كانت متباينة بشكل غير مألوف , اعتقد لورنز بداية إن عطل ألمّ بحاسبته لكنه بعد إعادة الحسابات اكتشف السبب،كان لورنز قد قرب النتائج ذات الست مراتب عشرية إلى ثلاثة لكنه لم يكن يتوقع إن مقدار كـ(0.0001) قد يحدث هذا الخلل الشاسع حيث كان لورنز يعتقد بصحة مبدأ التقارب آنف الذكر , بعد دراسة مستفيضة للنظام الرياضي الذي كان يستخدمه اكتشف سبب التباين إنه ( اللادورية )،لو كان الطقس يتسم بالدورية لمرة واحدة لكان الطقس يعيد نفسه بفترات زمنية ثابتة ولا حاجة عندها للتنبؤ عبر لورنز عن هذا لاحقاً بقوله “إن النظم التي لا تتسم بالدورية يستحيل أن تكون مجال للتنبؤ طويل الأمد” .
في عام 1963 قدم لورنز محاضرة بعنوان “هل تحدث رفرفة اجنحة فراشة بالبرازيل إعصار في تكساس” أطلق على الحساسية للشروط الأولية لاحقا ً (تأثير الفراشة ـ butterfly effect) كإشارة لمحاضرة لورنز .
يَعِد ديفد سالسبورغ (عضو الجمعية الأمريكية للإحصاء) بكتابه (ذواقة الشاي ـ كيف احدث الإحصاء ثورة بالقرن العشرين ) يَعِد لورنز واضع لنظرية الفوضى لكنه يدعي إن النماذج الفوضوية ظهرت عام 1980 بينما بين أيدينا ورقات بحثية أحدها منشور بمجلة (Natur) لـ R. M. May عام 1976 يتحدث عن سلوك فوضوي لأنظمة ديناميكية , و بحثJ.A Yorke مشاركة مع T. Y. Li الشهير (Period three implies chaos) عام 1975 , كما إن ورقة لورنز نفسه البحثية (Deterministic nonperiodic flow) المنشورة في (journal of the atmospheric science) عام 1962 تثير تساؤلات حول هذا التاريخ .
يعد سالسبورغ (تأثير الفراشة) بأنه “تصريح إيماني ليس إلا , له نفس القدر من القيمة والصحة العلمية كما لوجو الشياطين أو الإله” (سالسبورغ ـ ذواقة الشاي) وهذا ما سنناقشه بعد قليل .
الفوضى والعشوائية
ما هو الفرق بين بيانات لها سلوك عشوائي وأخرى لها سلوك محكوم بقوانين بسيطة لكنها ذات تكرار يعطيها سلوك غاية في التعقيد لنتأمل مجموعتين من البيانات بحجم 500
R= { 0.2190 0.0470 0.6789 0.6793 0.9347 0.3835 0.5194 0.8310 0.0346 0.0535 0.5297 0.6711 0.0077 0.3834 0.0668 0.4175 0.6868 0.5890 0.9304 0.8462 0.5269 0.0920 0.6539 0.4160 0.7012 0.9103 0.7622 0.2625 … }
D = { 0.9134 0.3164 0.8652 0.4666 0.9955 0.0178 0.0698 0.2596 0.7688 0.7110 0.8219 0.5855 0.9707 0.1136 0.4028 0.9622 0.1456 0.4975 1.0000 0.0001 0.0004 0.0016 0.0063 0.0250 0.0975 0.3521 0.9125 0.3193 0.8694 … }
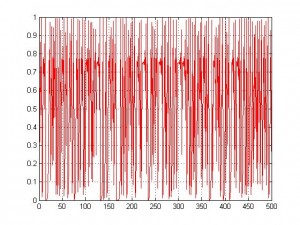
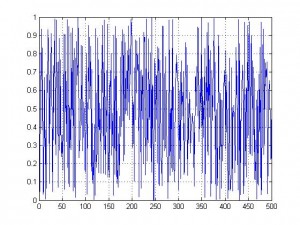
للاختصار لم أورد البقية لكني سأبينها بالرسم , كلا المجموعتين بين الـ 0 والـ 1 , رسمهما على ورق الرسم يعطيك انطباع إنهما مجموعتين عشوائيتين , لاحظ .
R1
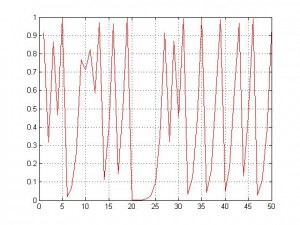
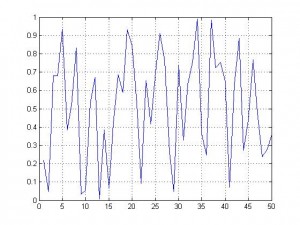
لكن لو تأملنا أول 50 رقم من كلا المجمعتين
D2
R2
نستطيع أن نلاحظ تراتب نسبي في الرسم D2 حيث إن طريقة صعود المنحني في الفترة الزمنية20 و25 توحي لنا بشبه نظام كذلك سلوك المنحني بعد الخطوة الزمنية 30 أشبه بالصعود والنزول المنتظم الأمر الغير موجود في الرسم R2 الحقيقة إن البيانات R ولدتها بصورة عشوائية تتبع التوزيع المنتظم في الفترة (0,1) أما البيانات D فولدتها بواسطة تكرار معادلة بسيطة تدعى المعادلة اللوجستية (logistic map) وهي Xt+1=4Xt(1-Xt) جرب أن تأخذ القيمة الأولى 0.9134 وأدخلها بالمعادلة كـ Xt لتحصل على القيمة الثانية وبإدخالها بالمعادلة ستجد القيمة الثالثة وهكذا إلى القيمة رقم 500 ثم ارسم النتائج ستحصل على الرسم D1 , السؤال كيف لنا أن نتأكد إن بيانات معينة عشوائية وليست فوضوية أو العكس والجواب هو إن رياضياتيين كبار مثل بيرسون وفيشر وجيرزي نيمان أفنوا سنوات عمرهم بتطوير اختبارات عشوائية البيانات والتي تحكم بعشوائية بيانات معينة من عدمها كما إن رياضياتي روسي أسمه ليبونوف أوجد أس ليبنوف (Lyaponv exponent ) الذي بإمكاننا الحكم بواسطته على فوضوية البيانات , لكن ألا يثير هذا التقارب بين نتائج تسلك سلوك رياضي محدد ونتائج عشوائية شيء من الأمل! بأنه يمكننا بيوم ما إيجاد نموذج رياضي للبيانات العشوائية ـ ولن تكون عشوائية حينها .
هل تحدث رفرفة فراشة إعصار ؟
لنشاهد الرسم التالي
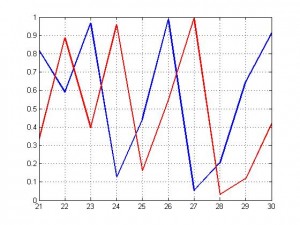
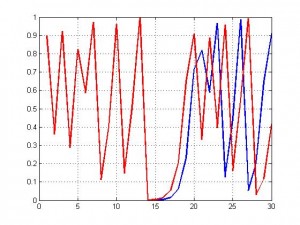
كم هو الاختلاف بين المنحنيين الأزرق والأحمر , لا يختلف اثنان على إنه كبير جدا ً , ماذا لو ادعيت إن كلا المنحنيان يسلك سلوك رياضي واحد ويخضعان للمعادلة اللوجستية نفسها في أعلاه , قد يتهمني أحدهم بالكذب أو التخريف لكنه قد يتمادى أكثر إذا أخبرته إن الفرق بين النقطتين الابتدائيتين هو فقط ( ( 0.000001 واحد بالمليون وإليك الدليل بالرسم التالي
الرسم الأول لمقطع اخترته من الرسم الثاني بين الـ 20 و 30 , الملاحظ إن الخطين متطابقان تماماً حتى قبل الخطوة الزمنية 15 لكنهما يفترقان بشكل صغير بعدها حتى يستحيل الفرق هائل لدرجة تجعلنا لا نصدق إنهما كانا متساويين تقريباً قبل فترة زمنية قصيرة نسبياً .
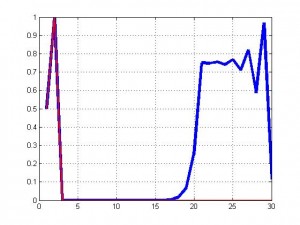
إذا أخذنا بعين الاعتبار إن المعادلة اللوجستية تنمذج نمو مجتمعات معينة فإن فرق طفيف كـ 0.000001 بتعداد مجتمعين مختلفين قد يتمخض عنه انقراض أحدهما في ما يستمر الأخر بالنمو , خذ القيمتين الابتدائيتين 0.5 و 0.500001 وتأمل الرسم
لاحظ إن المنحني الأحمر الذي يمثل نمو المجتمع ذو القيمة الابتدائية 0.5 يقفز إلى القيمة 1 ثم ينحدر إلى 0 ويبقى عندها بمعنى انه سينقرض بعد قفزتين زمنيتين أما المنحني الأزرق الذي يمثل المنحني ذو القيمة الابتدائية 0.500001 فيقفز لقيمة قريبة من الواحد ثم يأخذ قيم صغيرة قريبة من الصفر ثم يعود ليتصاعد بعد القفزة الزمنية 15 مما يؤشر إلى أن المجتمع الثاني سيمر بأزمة ولكنه سيتعافى منها بسبب الـ 0.000001 .
حساسية الشروط الأولية هذه تذكرني بإحدى وصايا بطل العرب الأول (سخرية طبعا )صدام حسين ! التي كنا نجبر على حفظها عن ظهر قلب أيام المتوسطة والإعدادية ( فكلمات القائد تسبق التحصيل العلمي يوم ذاك) , “لا تستهن بالبسيط الذي يصيب سمعتك فكم من حصاة صغيرة هشمت زجاجة كبيرة ” .