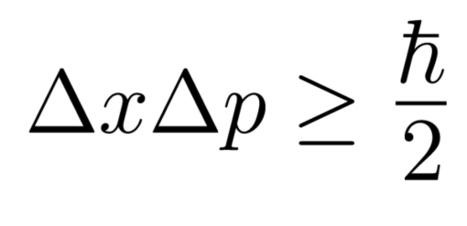كما نعلم من الفيزياء الكلاسيكية -فيزياء ما قبل أينشتين- أنه بإمكاننا القيام بقياسات بقيمة ضئيلة من عدم اليقين لدرجة تجاهلها، مما يعني التأكد بشكل تقريبي لل100% من حقيقة القياسات. ولكن مهلًا! للفيزياء الحديثة رأي آخر. وبالأخص ميكانيكا الكم. في عام 1927م قدّم العالِم الألماني (فيرنر هايزنبرج) مبدأ من أهم أساسيات ميكانيكا الكم الآن وهو مبدأ عدم اليقين (Uncertainty principle). باختصار مبدأ عدم اليقين ينص على أن: “إن كان عدم اليقين لموضع (مكان) جُسيم يساوي  ∆xو في نفس الوقت عدم اليقين لكمية حركته يساوي ∆P، فإن حاصل ضربهما لا يُمكن أن يقل عن h bar مقسومًا على 2.”

h bar تساوي ثابت بلانك مقسومًا على 2π. ثابت بلانك ((h = 6.626 x 10-34 جول.ثانية.

كان (هايزنبرج) حريصاً على إيضاح أن السبب في هذا العدم يقين لا يرجع لأخطاء في طرق قياسنا أو عيوب في أدوات القياس، بل السبب هو التركيب الكمي للمادة! إذن إنه حتمًا أمر خارج عن إرادتنا البشرية.

دعنا الآن نوضّح مصطلح “عدم اليقين”: فلنفترض أن نجارًا قام بقياس طول قطعة خشبية وقال أن طولها 2 متر مع عدم يقين -نسبة خطأ- 3 سنتيمتر، أي أن طول قطعة الخشب ايجازًا ممكن أن يكون أي قيمة بدايةً من 1 متر و 97 سنتيمتر إلى 2 متر و 3 سنتيمتر. ولكن هنا الموضوع مختلف قليلًا، لأن في حياتنا اليومية وعلى مقياسنا، فيمكن أن يكون سبب عدم اليقين في هذا المثال هو خطأ في طريقة القياس أو أداة القياس، ولا شرط أن يعود هنا للطبيعة الكمية للمادة. مبدأ عدم اليقين يُطبّق على المقياس الكمي كالإلكترون وليس على قطعة خشب طولها تقريبًا 2 متر!

لفهم مبدأ عدم اليقين، دع العنان لخيالك ودعه يتخيل جُسيم له “طول موجي وحيد ثابت” وأنت تعرف قيمة هذا الطول الموجي. وفقًا لعلاقة (دي برولي)، فإن الطول الموجي يساوي ثابت بلانك (h) مقسومًا على كمية الحركة (P)، تذكر أنك تعرف قيمة الطول الموجي للجُسيم الذي بخيالك، إذن يمكنك بكل سهولة حساب كمية الحركة للجُسيم (P) من خلال قسمة ثابت بلانك على الطول الموجي(1).

وفي الحقيقة الموجة ذات “طول موجي وحيد ثابت” -كما التي في خيالك- لا يمكن تفرقة أي نقطة عليها من أي نقطة آخرى لتحديدها ك”موضع” للجُسيم ، أي أن جميع النقاط خلال الموجة متماثلة لأن جميع أطوالها الموجية متماثلة، كما هو مُوضّح بالشكل(أ).

شكل أ

لذلك فإن عدم اليقين لموضع الجسيم هو لا نهائي فإنه يوجد في كل مكان خلال الموجة(2).

من (1) نعلم أن الجسيم له عدم يقين في كمية الحركة ضئيل للغاية.

من (2) نعلم أن الجسيم له عدم يقين في موضعه لا نهائي.

وهكذا، معرفتنا بكمية حركة الجسيم في البداية بدقة عالية، كلفتنا كل المعلومات الخاصة بموضعه.

والآن دع العنان لخيالك ثانيةً ودعه يتخيل جُسيم له نطاق من كمية الحركة، أي ليس له كمية حركة واحدة محددة(3). ووفقًا لعلاقة (دي برولي) للجُسيم أيضًا نطاق من الطول الموجي نتيجة لأن الجُسيم له نطاق من كمية الحركة، أي أن موجة الجُسيم لها “أطوال موجية مختلفة” وليس طول موجي وحيد فحسب.

تخيل أن الموجة ذات الأطوال الموجية المختلفة هي نتيجة لتداخل عدد من الأمواج. والمنطقة الصغيرة الناتجة عن التداخل البنّاء -أي أن قمم معظم أو كل الأمواج المتداخلة تتقابل في منطقة واحدة مكونة موجة ذات قمة هي الأكبر من كل قمم الأمواج المتداخلة- تُسَمى “حزمة ضوئية”. وهذه الحزمة الضوئية مكانها مميز خلال الموجة لأنها ذات القمة الأكبر كما هو مُوضّح بالشكل(ب).

شكل ب

وفي الفيزياء يمكننا تعريف الحزمة الضوئية ك”جُسيم” لأن هذه الحزمة لها خاصية أن يكون لها موقع في الكون كال”جُسيم”. لذلك موقع الحزمة الضوئية هو موقع “الجُسيم” الذي في خيالك الآن(4).

من (3) نعلم أن الجُسيم له عدم يقين في كمية الحركة كبير نظرًا لامتلاك عدد كبير من القيم لكمية الحركة وليس قيمة وحيدة محددة.

من (4) نعلم أن الجُسيم له عدم يقين لموضعه أو مكانه ضئيل للغاية.

إذن مرة ثانيةً، معرفتنا موضع الجُسيم بدقة عالية كلفتنا في البداية كل المعلومات عن كمية حركته.

كلما قمت بقياس كمية الحركة لجُسيم بدقة عالية، فإنك تفشل في تحديد موضعه بدقة، والعكس صحيح. وهكذا لا نستطيع قياس كلًا من كمية حركة جُسيم وموضعه بدقة عالية في نفس الوقت. نعم، إنها علاقة عكسية.

ملحوظة: لا تستنتج بالخطأ بأن مبدأ عدم اليقين ناتج عن تفاعلنا مع النظام الذي نرصده، على سبيل المثال: خلال تجربة افتراضية، قمت باستخدام ميكروسكوب بصري لرصد إلكترون، ولكن فوتون من الضوء الساقط على الإلكترون تصادم به وجعل الإلكترون يتحرك مما يعني عدم يقين في كمية حركة الإلكترون، لأنها بنسبة كبيرة كانت بسبب فوتون الضوء الساقط عليه لرصده! إذن عملية رصدنا للإلكترون أثّرت على كمية حركته. ولكن رغم أن هذا له علاقة بعدم اليقين في كمية الحركة، إلا أنه لا يوضح أساس مبدأ عدم اليقين. مبدأ عدم اليقين لا علاقة له بعمليات القياس أو الرصد، ولكنه يعتمد فقط على الطبيعة الموجية والكمية للمادة بدون أي تدخل منّا.

تذكّر: دع العنان لخيالك دائمًا.

المصادر:

Physics for scientists and engineers with modern physics by Serway and Jewett

Alok Jha, “What is Heisenberg’s Uncertainty Principle?“, 10 Nov 2013, theguardian.com

“What is Heisenberg Uncertainty Principle Formula | Quantum Physics“, February 21, 2018

ندى عفت محمود