هنالك فرعٌ من فروع الفيزياء يُعرف بالفيزياء الإحصائية، ويهتمُ هذا الفرع إهتماماً جذرياً بالحرارة، حيثُ يدرس هذا الاختصاص خواص انتقال الحرارة وتحوُلاتها إلى طاقات أخرى، حيثُ تتم صياغة القوانين التي تحكُم ذلك باستخدام ما يُسمى الميكانيكا الإحصائية. هذا الفرعُ يُسمى “الديناميكا الحرارية” أو “التحريك الحراري”.
ولكن أولاً لنتعرف على الحرارة وأهم المُصطلحات التي تخُص الفيزياء الحرارية بوجه عام:
ـ الحرارة شكل من أشكال الطاقة، وقد تنشأ الحرارة عن الحركة سواء كانت حركة جزيئات أو ذرات، أو عن الإشعاع الكهرومغناطيسي، أو عن التفاعُلات النووية أو الكيميائية.
وعلى النظير فدرجة الحرارة هي تكميم للحرارة (مُؤشِر لكمية الطاقة الحرارية). وتوجد العديد من مقاييس درجة الحرارة أشهرها على الإطلاق مقياس سيليزيوس ومقياس فهرنهايت ومقياس كلفن.

صورة توضح العلاقة بين السيليزيوس والفهرنهايت والكلفن
ـ وهناك ما يُسمى بالحرارة النوعية وهي كمية الحرارة اللازمة لرفع درجة حرارة واحد كيلوجرام من المادة بمقدار درجة واحدة مئوية.
ـ أيضاً السعة الحرارية أو التحميل الحراري وهي ببساطة قيمة تُوضح مدى قابلية المواد لتخزين الطاقة الحرارية. أو هي قيمة مُعينة من الطاقة يحتاجها الجسم أو النظام لرفع درجة حرارته درجة واحدة مئوية.
ـ التوصيل الحراري هو مُعَدَل مرور الطاقة الحرارية خلال مادة مُعينة، ويتم التعبير عن التوصيل الحراري بمقدار الحرارة التي تنساب لكل وحدة زمن خلال وحدة المساحة، مع تَدَرُج حراري بمقدار درجة واحدة لكل وحدة طول من المادة.
هناك مواد جيدة التوصيل للحرارة وتكون مقاومتها للحرارة ضئيلة جداً مثل الحديد النحاس الألومنيوم وغيرها من المواد. ولكن أيضاً هناك مواد رديئة التوصيل للحرارة وتُعرَف على أنها مواد ذات مقاومة حرارية كبيرة نسبياً مثل الصوف، والصخور. وتستخدم هذه المواد المواد رديئة التوصيل في العزل الحراري للأبنية والملابس وأواني الطهي.
أما الإنتقال الحراري؛ فيُمكن أن تنتقل الحرارة من جسم إلى آخر، أو من جسم إلى الوسط عن طريق واحدة من ثلاث طُرق وهُم:
- التوصيل المُباشر وهو عبارة عن انتقال الطاقة الحرارية خلال المواد عندما يتم توصيلها ببعضها بطريقة مُباشرة وبدون مسافات فاصلة.
- الحِمل الحراري وهو عبارة عن انتقال الطاقة الحرارية خلال وسط مائِع (سوائل ـ غازات).
- الإشعاع الحراري وهو إنتقال الطاقة الحرارية خلال إشعاع كهرومغناطيسي، حيث تتولى الفوتونات مهمة نقل الطاقة.
كما وتنقسم العمليات الديناميكية إلى عدة أنواع وهى:
- عملية متساوية الضغط وهي العملية التي تتم تحت ضغط ثابت.
- عملية متساوية الحجم وهي العملية التي تتم تحت حجم ثابت.
- عملية متساوية الحرارة وهي العملية التي تتم تحت درجة حرارة ثابتة.
- عملية كظومة أو كاظمة وهي العملية التي تتم في النظام المعزول حرارياً عن الوسط المُحيط به، أي لا يتم أي تبادل لا للطاقة ولا للمادة مع الوسط المُحيط.
- عملية متساوية الإنتروبي أو الاعتلاج وهي العملية التي تتم عند إنتروبي أو اعتلاج ثابت، أي أن الإنتروبي تأخذ قيمة ثابتة لا تزيد ولا تقل عنها. والانتروبي هي العشوائية أو مقياس لانعدام النظام.
- عملية متساوية الإنثالبي وهي العملية التي تتم عند محتوى حراري ثابت، والمحتوى الحراري هو مقياس للطاقة الكلية للنظام الثرموديناميك، ومن ضمنها الطاقة الداخلية للنظام بالإضافة إلى كمية الطاقة اللازمة لإفساح مكان (حجم) للنظام خلال الوسط المحيط وتهيئة النظام للحصول على حجمه وضغطه.
وهناك أيضاً النُظُم الحرارية. وهي جسم أو مجموعة من الأجسام المادية التي تتبادل الطاقة والمادة فيما بينها، أو مع الوسط المُحيط بها.
أما أنواعُ النُظُم الموجودة بالديناميكا الحرارية فهي:
- النظام المفتوح الذي يسمح بتبادل الطاقة والمادة مع الوسط المُحيط.
- النظام المُغلَق الذي يسمح بتبادل الطاقة دون المادة مع الوسط المُحيط.
- النظام المعزول الذي لا يسمح بتبادل كُلاً من الطاقة والمادة مع الوسط المُحيط.
وكأي علم له مبادئ معروفة، فإن للديناميكا الحرارية مبادئ أساسية، ومبادئ الديناميكا الحرارية تتلخص في عبارة “الحرارة شكل من أشكال الطاقة”، ولها أربعة قوانين في غاية الأهمية:
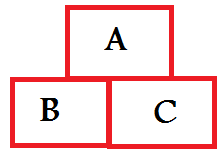
صورة توضح مفهوم القانون الصفري
القانون الصفري: إذا كان النظام (أ) مُتزن حرارياً مع النظام (ب)، والنظام (ب) مُترن حرارياً مع النظام (ج)؛ فإن النظام (أ) يكون مُتزن حرارياً مع النظام (ج). وكما نرى فإن هذا القانون يصف التوازن الحراري بين الأنظمة أو الأجسام. وجديرُ بالذكر أن هذا القانون سُمِّى بالقانون الصفري لأنه يُعَد معلومة بديهية معروفة أي كأننا نقول: القانون رقم صفر.
القانون الأول: الطاقة في أي نظام مُغلق تظل ثابتة. ويُعني ذلك أن الطاقة الداخلية للنظام تُساوي كمية الحرارة التي تدخل النظام مطروحٌ منها الشُغل الذي يبذله النظام، ويُمكن تسميته بقانون حفظ الطاقة الحرارية.
وإذا اعتبرنا الديناميكا الحرارية لُعبة فيُمكن اعتبار القانون الأول بمثابة قاعدة تنص على أنه “لا يُمكنك الفوز”، وذلك يُعني أنه بما أن المادة والطاقة لا يُمكن فناؤهما، فلا يُمكنك أن تحصل على إحداهما دون خسارة الاُخرى.
∆ U= ∆ Q- ∆ W
Δ U الطاقة الداخلية ΔQ الطاقة الحرارية Δw الشغل
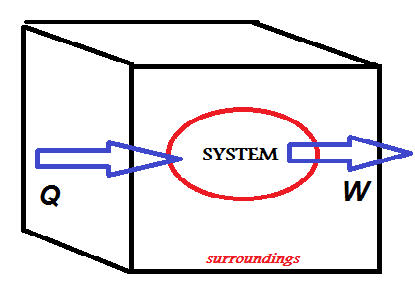
صورة توضح معنى القانون
القانون الثاني: التغيُّر التلقائي في أى نظام فيزيائي لا بُد وأن يُصاحبه زيادة في مقدار الأنتروبي، ويُعتبَر هذا النص أشهر نص للقانون الثاني.
والانتروبي: هي العشوائية، أو هي مقياس لعدم النظام، أي زيادة العشوائية. والقانون يقول أن العشوائية تسير تلقائياً وطبيعياً في اتجاه زيادة العشوائية أو أنها تظل ثابتة. فمثلاً، إذا أذبنا قليل من السكر في كوب من الماء النقي، فإنتشرت جزيئات السُكر وتوَزَّعت توزيعاً متساوياً في الماء. فإن هذه عملية طبيعية تسير تلقائياً، ونقول أن إنتروبي النظام قد ازداد؛ إذ أن مجموع إنتروبي السكُر + إنتروبي الماء النقي يكون أصغر من إنتروبي المخلوط. أي تزداد إنتروبي النظام بأكمله (السكر + الماء النقي) بمرور الزمن بعد الخلط. وإليكُم مثالاً آخر، تخيّلوا وجود عدة حصى صغيرة مُرتَّبة في تشكيل مُعين يسهُل التعرُّف عليه، ثُم قُمنا بفك هذا التشكيل إلى أن اصبحت الحصى مُبعثرة في الأرجاء. ببساطة إن العشوائية هي بعثرة الحصى، حيثُ عندما كانت الحصى مُرتَّبة ومُنسَّقة في تشكيل كانت العشوائية غير موجودة بالمرة، أما حين أصبحت الحصى مُبعثَرة زادت العشوائية بوضوح تام.
ولكن نظراً للتعريف الواسع الذي يتضمنه هذا القانون، يتصور كثير من الناس أن هذه الصيغة تعني أن القانون الثاني للحرارة ينطبق على كل شيء يمكن تخيُّلُه. لكن هذا ليس صحيحاً فالصيغة الجديدة ماهي إلا تبسيط لحقيقة أكثر تعقيدا، وهي أن الإنتروبي في الكون تميل إلى نهاية عُظمى. حيث يشمل ذلك الكون كله من دون أي تحديد لحالته. بقى أن نذكر أن العالِم الألماني “رودولف كلاوسيوس” هو الذي صاغ القانون الثاني.
وللتبسيط أكثر نعود إلى فرضية اللُعبة حيث يكون القانون الثاني بمثابة قاعدة تنص على أنه “لا يُمكنك التوقف”، وذلك يعني أنه بسبب زيادة الانتروبي لا يُمكنك العودة إلى لنفس حالة الطاقة، أى أن الطاقة المُتمركزة في مكان أو منطقة مُعينة ستنتشر دوماً نحو الأماكن ذات التركيز الأقل. والانتروبي هو مقياس ذلك الانتشار العشوائي في النظام.
d S ≥0
d S الإنتروبي
القانون الثالث: من المُستحيل تبريد نظام إلى درجة الصفر المُطلق (صفر كلفن).
من الواضح أن هذا القانون يُحدِّد درجة الصفر المُطلق كحد من حدود الطبيعة لا يُمكن تجاوُزُه، ولا يُمكن الحصول على أقل منه. ويرجع السبب إلى أنه كُلما قلت درجة الحرارة كُلما قلت حركة الذرات والعكسُ بالعكسِ. إذاً وصول درجة حرارة المادة للصفر المُطلق يُعني أن ذرات المادة أصبحت ساكنة تماماً، كما ويُعني أن يتلاشى الحجم، وهذا مستحيل !.
وبالعودة إلى فرضية اللُعبة فالقانون الثالث بمثابة قاعدة تنص على أنه “لا يُمكنك أن تخرج من اللعبة”، وذلك يشير إلى عدم المقدرة على الخروج إلى الوصول إلى الصفر المُطلق (-273.15 درجة مئوية).
صورة لطيفة عن مُجمَل قوانين الديناميكا الحرارية
من أبرز العُلماء الذين ساهموا في تقدم علم الديناميكا الحرارية: ويليام طومسون، هرمان فون هلمهولتز، سادي كارنوت، رودولف كلاوسيوس، جوزيه غيبس، ويليام رانكين.
والمُشادُ به أن التطبيقات القائمة على الديناميكا الحرارية كانت خيالاً علمياً وقصصاً تُروَى من زمنٍ بعيد. لكن الآن أصبحنا نرى وأحياناً نستعمل التكييفات، والمُبرِدات، والمُحرك البخاري، وغيرها من التطبيقات ذات النفع العظيم.
إن تطور العلوم لا حدودَ له. كما أن علم الديناميكا الحرارية مازال يشهد تطوراً ملحوظاً. والبشرية مازلت وسوف تزال في حاجة مُلِحَة إلى هذا التطور.
المصادر:
- INTRODUCTION TO MODERN STATISTICAL MECHANICS (David Chandler).
- George B. Arfken • David F. Griffing • Donald C. Kelly• Joseph Priest, Miami University, Oxford, Ohio (A Preview of Thermodynamics).
- “plankdover” reviewed and coordinated at 2017.
- Enrico Fermi (1956). Thermodynamics. Courier Dover Publications. pp. (ix).
- SERWAY.JEWETT; Physics For Scientists And Engineers (Part 3, Thermodynamics).
- Guggenheim, E.A. (1933). Modern Thermodynamics by the Methods of J.W. Gibbs, Methuen, London.
- STATICAL MECHANICS (KERSOH HUAHG).Schools of thermodynamics – EoHT.info.
- William Thomson, LL.D. D.C.L., F.R.S. (1882). Mathematical and Physical Papers. 1. London, Cambridge: C.J. Clay, M.A. & Son, Cambridge University Press. p. 232.
- “engineering thermodynamic 1993” reviewed at 2017.
- Perrot, Pierre (1998). A to Z of Thermodynamics. Oxford University Press.

