ولد ديفيد هيبلرت عام 1862 في مملكة بروسيا في مدينة تقع اليوم ضمن حدود روسيا الحالية، وهو عالم رياضيات الماني لامع عرف بالكثير من المنجزات ذات الأثر في الفيزياء والرياضيات. حصل على الدكتوراه في ثمانينات القرن التاسع عشر وعمل في جامعة كونيغسبيرغ (University of Königsberg) ثم في جامعة كوتنغن (Göttingen school) حتى نهاية حياته. وعرف بأعماله في نظرية الاثبات، حساب المتغيرات، الجبر التبادلي، نظرية الأعداد الجبرية، النظرية الطيفية وتطبيقاتها في المعادلات التكاملية، كما عرف بمعضلة الفندق وغير ذلك من الأعمال. ولو حاولنا الكتابة عن منجزات هيبلرت فلن يسع هذا المقال منجزاته، غير أن مما يلفت الانتباه في مسيرته هو ما حدث بينه وبين اينشتاين وهو ما سنركز عليه في هذا المقال.
من الغريب أن دخول هيبلرت في الفيزياء كان متأخراً في مسيرته العملية. حيث شرع بدراسة الفيزياء في العام 1912. وفي تلك الفترة كانت أعمال البيرت آينشتاين وغيره تنال الاهتمام الكبير في الساحة العلمية. وسرعان ما التقى اهتمام هيبلرت بالنظرية النسبية العامة لآينشتاين عام 1915 ثم حدث اللقاء بينهما اثر دعوة هيبلرت لآينشتاين. وبعد ذلك بوقت قصير أصدر هيبلرت بحثه “أساسيات الفيزياء”، والذي قدم فيه اشتقاقات بديهية لمعادلات الحقل (field equations) والتي هي معادلات تفاضلية جزئية تختص بتوضيح ديناميكيات حقل فيزيائي معين أي متجه معين او قيمة معينة على سبيل المثال. وكان هيبلرت بالإضافة لذلك رائداً في تقديم بديهيات جديدة في الرياضيات أصبحت خلفاً أو شرحاً وتوضيحاً لبديهيات اقليدس (من الأمثلة عليها: يمكن رسم خط مستقيم من أي نقطتين). وبديهيات هيبلرت التي خلفت بديهيات اقليدس توسعت لتشمل نطاقاً أوسع من الاجسام وليس ما يقوم على البعدين فحسب، فما ينطبق من بديهيات اقليدس على مستوي قد لا ينطبق في حال تطبيقه على الكرة.
عرف ذلك التداخل بين عمل البيرت واينشتاين بفعل آينشتاين-هيلبرت أو فعل هيبلرت (Einstein–Hilbert action) وتشير كلمة الفعل هنا فيزيائياً إلى قيمة عددية تصف تغير نظام فيزيائي معين مع الزمن. ومثلما أن هناك معادلات تفاضلية جزئية لمعادلات حقل معينة في الفيزياء فإن فعل هلبرت يختص بشرح النسبية العامة. ويشرح معادلات حقل آينشتاين، التي تربط بين هندسة الزمكان وتوزيع المادة ضمنها، مثلما تفعل نظريات فعل أخرى مع حقول أخرى مثل الحقل الكهرومغناطيسي لماكسويل. فإن معادلات الحقل لاينشتاين تربط بين هندسة الزمكان وتوزيع الكتلة والطاقة والزمن، ويتفرع من ذلك قضايا عديدة مثلاً كيف للمادة والزمن احداث انحناء في الزمكان، موجات الجاذبية وتوسع الكون المتسارع، وقد لخصها جون اركيبالد ويلر (John Archibald Wheeler) بقوله: “الزمكان يخبر المادة كيف تتحرك والمادة تخبر الزمكان كيف ينحني”.
تكمن أهمية فعل آينشتاين-هيلبرت في أنه يقدم شرحاً لمستوى رياضي جديد. على غرار الاختلاف الحاصل بين الهندسة المجسمة والسطوح المستوية حيث قدم هيبلرت بديهيات جديدة، فإن الزمكان هنا أيضاً يمثل مجالاً استثنائياً يحتاج لقواعده الخاصة في الهندسة.
تتألف معادلة فعل آينشتاين هيبلرت من ممتد (tensor) للقياس (g في المعادلة أدناه)، وقيمة للانحناء (متمثل بـ R في المعادلة أدناه)، تعرف أيضاً بقيمة ريتشي (Ricci Scalar)، بالإضافة الى ثابت الجاذبية لآينشتاين (متمثلاً بـ K في المعادلة أدناه).
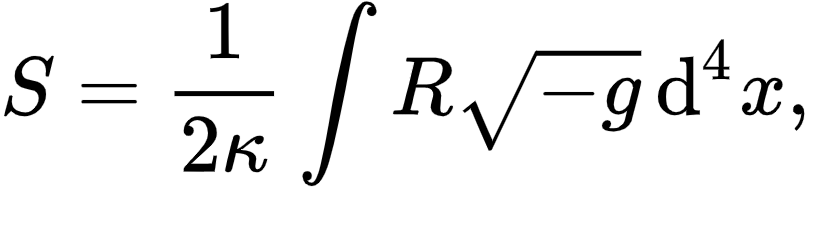
يرتكز فعل آينشتاين-هيلبرت الى مبدأ الفعل الأدنى في الفيزياء، والذي ينص على أن المسارات الحركية لفعل ما في نظام فيزيائي معين يتمثل بنقاط الثبات في دالة فعل النظام. ولتبسيط هذا قليلاً، يمكن القول أن المسار الحركي لفعل ما في نظام فيزيائي يجب أن يكون المسار الأقصر. وهذا المبدأ وارد في عدد كبير من الأنظمة في الفيزياء مثل قوانين نيوتن او قوانين هاملتون للحركة، او النظرية النسبية العامة لكن باختلاف الفعل في كل من هذه الحالات.
بالطريقة التي نرى فيها مساهمة هيبلرت في النسبية العامة، ودخوله المتأخر نسبياً في الفيزياء – امام مسيرته العلمية في الرياضيات – نجد حالة لا تتكرر كثيراً في العلم في القدرة على المساهمة بنظرية حديثة أحدثت ثورة في العالم ومن قبل عالم آخر من مجال موازي، على الرغم من تقارب طبيعة الطرح مع عمل هيبلرت بشكل عام. وعلى الرغم من مساهمة هيلبرت الهامة، فإن هيلبرت عزى الفضل فيما قدمه الى آينشتاين وأعتبره صاحب الإنجاز الوحيد لمعادلات الحقل، وهذا ما جعل الفعل يسمى بفعل هيلبرت آينتشاين (او العكس) فيما يصر البعض على عزوه لهيلبرت في خلاف بتأريخ ودراسة العلم وضمن مسألة تعرف بنزاع الأولوية حول النسبية العامة (General relativity priority dispute).
نشر هذا المقال ضمن مجلة العلوم الحقيقية العدد 56 وراجعته لغوياً ريام عيسى

